カメラの数理？

投稿日 2024-02-17 編集日 2025-12-03 Disqus：

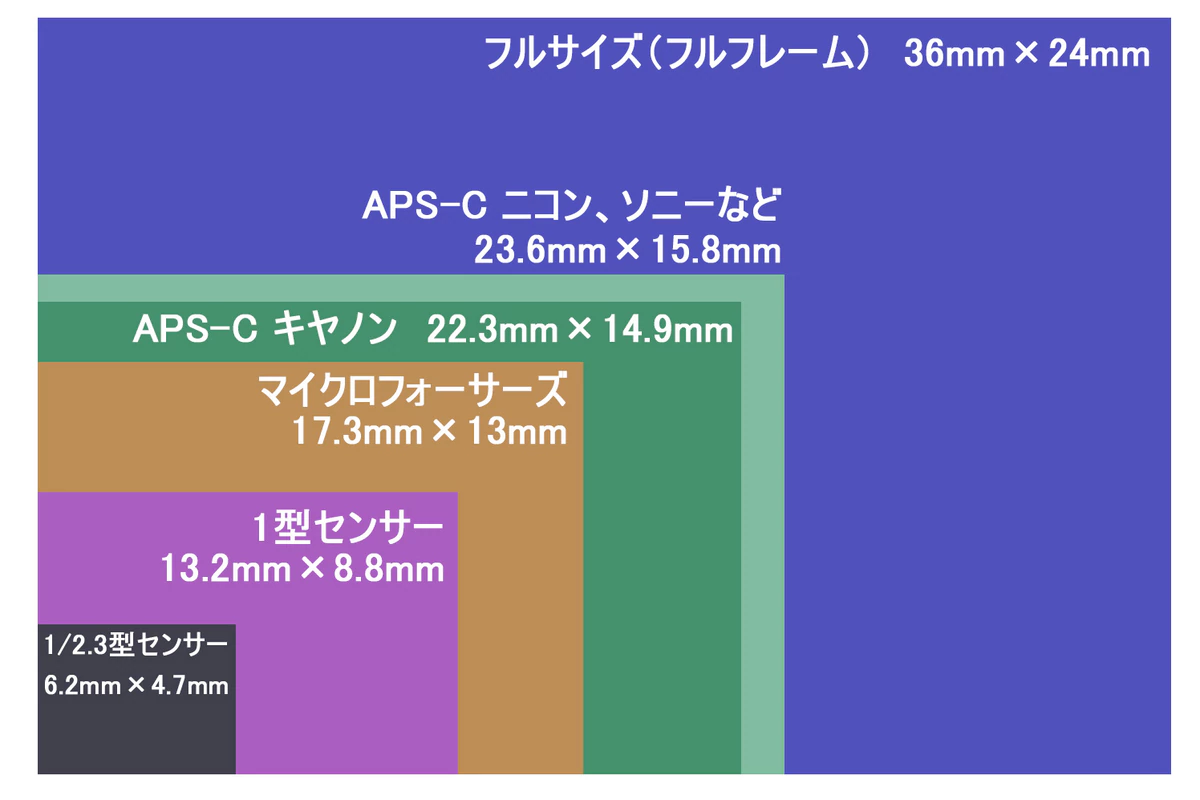
カメラのセンサーサイズ

幾何光学?

曲率一定の曲面による反射

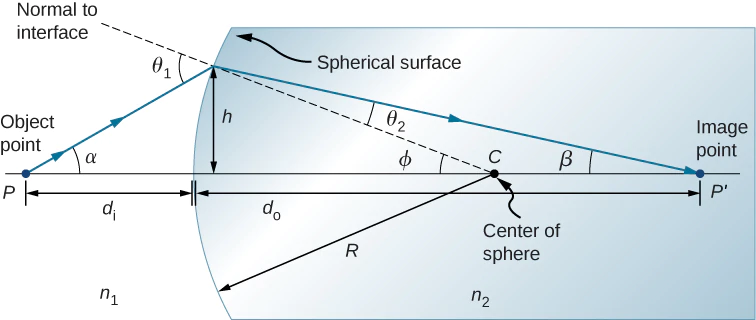
より

入射側,透過側の曲率(curvature)をR₁, R₂とし、u: 被写体距離, u′: 入射側より先の屈折率がnであったとしたときの焦点距離(thin lens approximation), u_o: 焦点距離とし、(u,u′,1,n), (u′,u_o,n,1)に対して上式を2度使いu′を消去すれば、以下の式が得られる。ガウスのレンズ公式証明 - あなばブログ

レンズメーカーの式(lensmaker’s equation)

レンズの公式(thin lens formula)

カメラレンズの焦点距離表示

「全群繰り出し」「フロントフォーカス」「リアフォーカス」「インナーフォーカス」の4種類がある。³ ⁴「全群繰り出し」は焦点距離が不変だが、その他は被写体距離に応じて焦点距離が変わる。これを「ブリージング」という。⁵ ⁶

F: カメラレンズの焦点距離表示,

$全群繰り出し$

F値

f: 焦点距離(focal length), N: F値(f-number), D: 有効口径(直径)(effective aperture)

画角

画角は像側、被写体画角は物体側の角度によって決まる。

α: 画角(angle of view, AOV), α_∞: 無限遠画角, d: 指定方向のセンサーサイズ

α′: 被写体画角, h: 被写体サイズ

ボケ(bokeh)

(u,v,f)がレンズの式を満たしている状態で、v′を焦点にもつ被写体距離u′の被写体のvにおける錯乱円直径(circle of confusion, COC)cを求めたい。相似を考えて

v′を削除すると以下のようになるらしい。

⁷ ここで錯乱円画角(独自用語)は

複数の被写体をボケずに写せるかどうかを調べたい。

DOF: 被写界深度(depth of field, DOF), u: 被写体距離(distance to subject)

⁸

背景ボケを調べたい。 b: 背景錯乱円直径(background blur disk radius)

光束/光量

H: 光束/光量, T: レンズ透過率, L: シーン輝度, v(θ): ケラレ係数

⁹

ノイズ

CMOSイメージセンサーは各フォトダイオードの信号をMOSFETを用いて増幅し、選択するという仕組みをとる。¹⁰フォトダイオードは光起電力効果によって動作する。コヒーレント光源では、光子数はs := n̄ = Δn²のポアソン分布に従う。これをポアソン光と呼び、分散が平均より大きい光をスーパーポアソン光、小さい光をサブポアソン光と呼ぶ。古典光はポアソン光かサブポアソン光であるので¹¹、ここではポアソン光を仮定する。

¹²によれば、RMSノイズNは、(ISO感度に比例する)増幅器ゲインG,増幅後信号S := Gs,増幅前ノイズn_r1,増幅後ノイズN_r2を用いて

$高時$

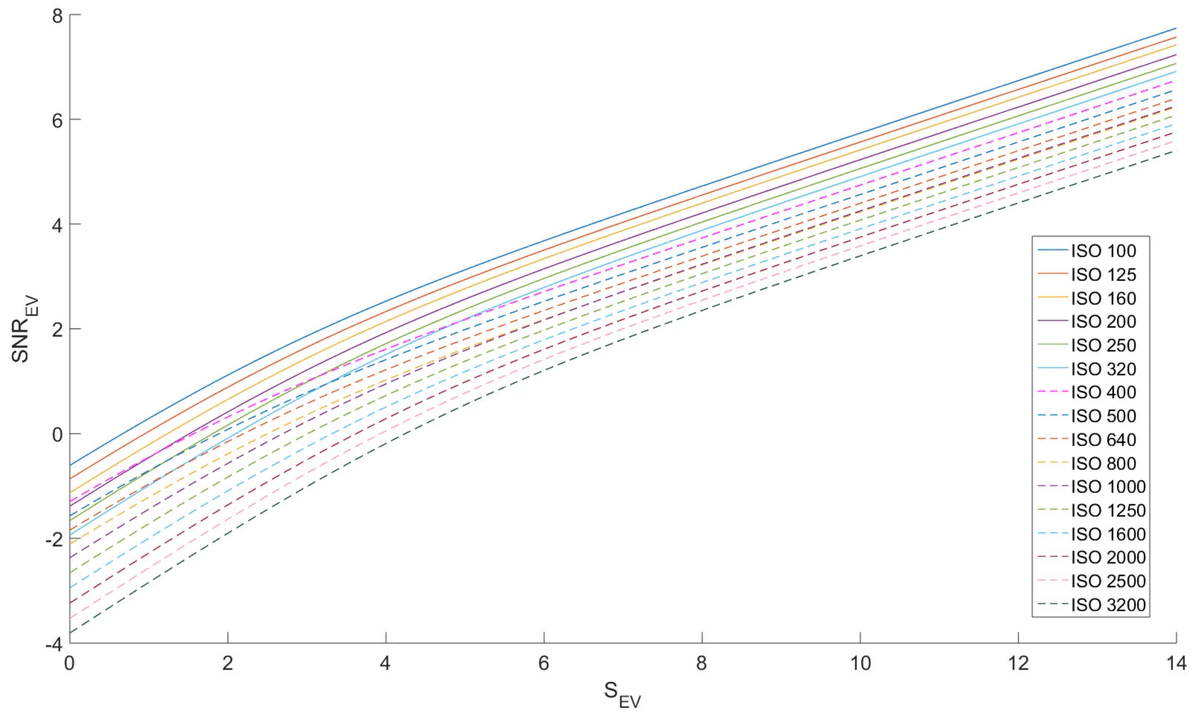
よって、十分に明るい場合（グラフの右側）、SNRはセンサーによらない。 Sを固定すると同じ明るさの写真が撮れるので、G, sを変数として考えると、Θ(G^−0.5)となる。一方で、十分に暗い場合（グラフの左側）、SNRはo(G⁻¹), O(1)となる。下のグラフを見る限りではISO 3200 → 640でlog₂SNRは − 4 → − 2となっているので、よりおよそΘ(G^−0.86)である。いずれにせよISO,GはSを固定したときにSNRを下げる要素であるため、小さい方が良い。

Canon 50D(APS-C,2008年発売)におけるノイズの測定値

¹³によれば、G_{ISO = 100} = 0.447であり、はおおよそ満たされていた。また、

とある。sの単位は恐らく光子数=電子数e⁻である。(光電効果では1光子につき1電子。)しかし、これだけでは光量Hと光子数sの関係が不明であるため、なんとも言えないと思う。センサー効率を1, 視感度を1(ν = 555nmの単色光)とし、光量と仕事率の比例定数をϕとすれば(1ルーメンは1/683W¹⁴)、shν = ϕHとなるので……？ Nikon D500 SNR curves for ISOs

¹⁵

n倍するもの	被写体の占める画角α	背景の占める画角α_∞	1センサー当たり明るさS	被写界深度DOF	背景ボケ	SNR(S固定)	価格(主観)
センサーサイズ(解像度固定)	1/n	1/n	n^2	n	1/n		n(新品)?, 1(中古)? (EOS 6D(フルサイズ, 198k, キタムラB 47.6k)とEOS 70D(APS-C, 94.8k, キタムラB 39.2k)の比較による)
センサー画素密度(センサーサイズ固定)	1	1	1/n^2	1	1		n?
有効口径(レンズ固定時のF値の逆数)	1	1	n^2	1/n	n		?
焦点距離	n	n	1/n^2	1/n	n		1 (望遠以外)?
シャッタースピード	1	1	n	1	1		1
ISO感度	1	1	n	1	1	n	1
レンズ透過率(NDフィルター)	1	1	n	1	1		1
輝度(ストロボ)	1	1	被写体のみn	1	1		n?
被写体との距離	1/n	1	1	n^2	1/n		1

帰結

要するに1つのパラメータを変えて、他のパラメータを変更することにより元通りの写真が撮れるかを検討したいわけである。これらの値をlog_nしたものによるベクトルの(部分)集合が張るℝⁿ上の部分空間で線形代数ごっこをすると（別に線形代数を持ち出さなくても良いが）いくつかの結論が得られる。

センサーサイズを小さくすると、被写体に近づいて[圧縮効果減少(かつ遠近歪み)]を起こすか、焦点距離を下げて[被写界深度の上昇(=背景ボケの低下)]を起こさなければならない。更に同じ解像度を用いる場合、センサー画素密度が上がるため、1センサー当たり明るさを上げる必要があり、これ以上レンズ透過率・シャッタースピードを上げられない場合、[ノイズの上昇]がより多く起こる。
ストロボは被写体の明るさと背景の明るさの比を変えるための唯一のパラメータである。
明るさを変えるためのパラメータがとても多い。